Extended Wall Decorations

The author of ConfluxIII demanded that we make it possible to define additional wall decorations. In order to provide the necessary variety in his dungeon, he had been forced to produce additional wallsets for his skins; an extremely tedious and wasteful process. Here is the result: the ability to display up to 262,000 different wall decorations arbitrarily on any level of the dungeon.

Specifying wall decoration locations -

Ah! The DSA becomes valuable again! Actuators commonly specify a wall decoration. For example, a pushbutton might specify that a 'Blue Button' be displayed on the wall. Normally, a DSA has no decoration. But! If the DSA is number 255, then its parameter A is used to specify a wall decoration from the CSBgraphics.dat file.

Format of Wall Decorations -

A Wall Decoration consists of three parts:

  1. An array of descriptors showing where the decoration should be displayed on each of 13 walls that the player can see while touring the dungeon.
  2. A bitmap of the side view of the decoration
  3. A bitmap of the front view of the decoration.

A 'Wall Decoration' segment of CSBgraphic.dat consists of those three parts, one after the other, with any padding necessary to make each part start on a four-byte boundary. (2 bytes of zero are needed between parts one and two. Parts two and three are, by definition, a multiple of four bytes in length and so no padding is necessary between them.) The two bytes of zero should be set to ZERO because we may find some use for them someday.

The positioning Descriptors -

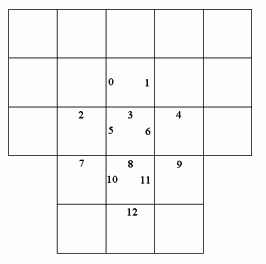
There are thirteen descriptors; in numeric order, for each of the numbered positions shouwn in this diagram:

Wall Numbers

Each descriptor consists of six bytes of information providing the x and y coordinates of a rectangle, relative to the viewport, which is to contain a view of the Wall Decoration.

Descriptor 11 describes the 'side-view' bitmap and descriptor 12 descripes the 'front-view' bitmap.

The Bitmaps -

The bitmaps are in the Atari 'Bit-Plane' format in which four 16-bit words are used to represent 16 pixels. The first of the four words contains the least significant bit of each of the 16 pixels. The second 16-bit word contains the next least significant bits, etc. The most significant bit in each of the four words provide the four bits for the first pixel, etc. In this way the four words define 16 pixels. Each horizontal line in the bitmap contains a multiple of four words or sixteen pixels.

Rectangles used by Dungeon Master

Here are all the rectangles used by Dungeon Master to display Wall Decorations. There are eight groups of thirteen. Each decoration in the dungeon specifies which group is to be used to display that decoration. This was done so that each decoration would require only one byte to specify the placment. In our case, it seemed reasonable to add the 78 bytes of information to each of the decorations and, in return, we can place them arbitrarily . . . even totallly mis-place them if that helps your design in some way.

50 53 29 2D 08 05
8C 8F 29 2D 08 05
10 1D 27 32 08 0C
6B 78 27 32 08 0C
BB C8 27 32 08 0C
43 4D 28 31 08 0A
92 9C 28 31 08 0A
00 11 26 37 10 12
66 7B 26 37 10 12
CE DF 26 37 10 12
30 3F 26 38 08 13
A0 AF 26 38 08 13
60 7F 24 3F 10 1C


4A 52 29 3C 08 14
8D 95 29 3C 08 14
01 2F 25 3F 18 1B
58 86 25 3F 18 1B
AB D9 25 3F 18 1B
3D 4C 26 43 08 1E
93 A2 26 43 08 1E
00 2B 25 49 20 25
50 8F 25 49 20 25
B4 DF 25 49 20 25
20 3F 24 53 10 30
A0 BF 24 53 10 30
40 9F 24 5B 30 38


50 53 42 46 08 05
8C 8F 42 46 08 05
10 1D 40 4B 08 0C
6A 77 40 4B 08 0C
BB C8 40 4B 08 0C
43 4D 4A 53 08 0A
92 9C 4A 53 08 0A
00 11 49 5A 10 12
64 79 49 5A 10 12
CE DF 49 5A 10 12
30 3F 54 66 08 13
A0 AF 54 66 08 13
60 7F 5C 77 10 1C


50 53 31 35 08 05
8C 8F 31 35 08 05
10 1D 32 3D 08 0C
6A 77 32 3D 08 0C
BB C8 32 3D 08 0C
43 4D 35 3E 08 0A
92 9C 35 3E 08 0A
00 11 37 48 10 12
64 79 37 48 10 12
CE DF 37 48 10 12
30 3F 39 4B 08 13
A0 AF 39 4B 08 13
60 7F 40 5B 10 1C


4B 5A 28 2C 08 05
85 94 28 2C 08 05
01 30 2C 31 18 06
58 87 2C 31 18 06
AB DA 2C 31 18 06
3C 4D 28 2E 10 07
92 A3 28 2E 10 07
00 23 2B 32 20 08
50 8F 2B 32 20 08
B8 DF 2B 32 20 08
20 3F 29 34 10 0C
A0 BF 29 34 10 0C
40 9F 29 34 30 0C


4E 55 24 33 08 10
8A 91 24 33 08 10
0A 29 22 35 10 14
62 81 22 35 10 14
B3 D2 22 35 10 14
42 4B 22 38 08 17
93 9D 22 38 08 17
00 1A 21 3D 18 1D
5B 85 21 3D 18 1D
C2 DF 21 3D 18 1D
29 38 1F 41 08 23
A7 B6 1F 41 08 23
50 8F 1D 47 20 2B


4B 52 19 4B 08 33
8E 95 19 4B 08 33
0C 3C 19 4B 20 33
58 88 19 4B 20 33
A3 D3 19 4B 20 33
40 49 14 5A 08 47
96 9F 14 5A 08 47
00 26 14 5A 20 47
52 8E 14 5A 20 47
B8 DF 14 5A 20 47
29 38 09 77 08 6F
A9 B8 09 77 08 6F
40 9F 09 77 30 6F


4A 55 19 4B 08 33
89 95 19 4B 08 33
00 53 19 4B 30 33
4A 95 19 4B 30 33
8B DF 19 4B 30 33
3C 4D 14 5A 10 47
92 A3 14 5A 10 47
00 4A 14 5A 38 47
3C A3 14 5A 38 47
95 DF 14 5A 38 47
20 3F 09 77 10 6F
A0 BF 09 77 10 6F
20 BF 09 77 50 6F